エピポーラ幾何

OpenCVでステレオカメラのキャリブレーションを行うと、引数にEssential MatrixやらFundamental Matrixやら出てきてわからなかった。
英語の文献を読むとわかりやすかった。分かれば大したことないかもしれんけど、ぼくみたいな誰かの参考になるようここにメモっておこう。

参考文献：　http://www.robots.ox.ac.uk/~vgg/hzbook/hzbook1/HZepipolar.pdf



ではエピポーラ幾何について話す。
下の図のようにカメラが２つあって、どちらにも点Pが写っているとする。

左のカメラから見た点が、右のカメラのどの座標に写っているかが分かれば、
△OlOrPからPの深さが分かる。

しかし、実際はその対応関係がわからない（下図）。
対応付けをするためには、画素を調べて同じ点を探す必要がある。



しかし、2次元画像のすべての画素の対応を調べる必要はない。
２つのカメラの位置関係がわかっていれば、
その探索は1次元（エピポーラライン上）で済む。

ではその理由を数式を用いて探っていく。
△OlOrPの形は定かではないが、
,


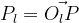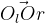
は同じ平面上にあるという制約（Epipolar constraint)がある。
よって以下の式が成り立つ。



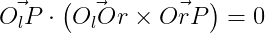
これを左のカメラの座標で書き直すと



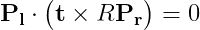
ｔ、Rは右の座標から左の座標へのtranslation vectorとrotation matrix。
ここで外積はベクトル→ベクトルの変換なので等価な行列表記にすると以下のようになる。





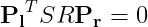
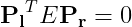
このEがEssential Matrixで、Rとt（カメラの外部パラメータ）から成り立っている。

これはフィルム上の点でも成り立つ。つまり



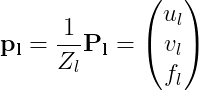
などとフイルム上の座標を表記したとき、



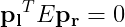
が成り立つ。


Fundamental Matrixはにカメラの内部パラメータも押し込んだ形のものだ。
フィルム座標からピクセル座標への変換はAffine transform matrix以下のように表せる。



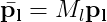
これを上の式に代入すると、





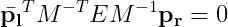
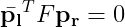
Fはカメラの外部パラメータ、内部パラメータをひっくるめたものであることがわかる。

で、ここから何がわかるかだ。

ピクセル座標での直線を考えるよう。直線の方程式は以下のようになる。




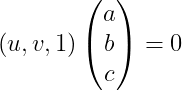
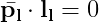
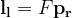とおくと上のFundamental Matrixの式と同じになる。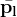がライン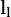上にあることを示している。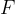はカメラの構成によってのみ決まるので、どちらかのピクセル座標を与えれば、どのライン上にもう片方のピクセルが存在するか決めることができる。


OpenCVに実装されているので、実際に計算することはないと思うけど、意味は知っておきたいですね。